数据结构-树

注:图片源自极客时间的数据结构与算法之美专栏

树

---

类似于现实生活中的树,每个元素叫做节点;用来连线相邻节点之间的关系,我们叫做父子关系.

基本概念

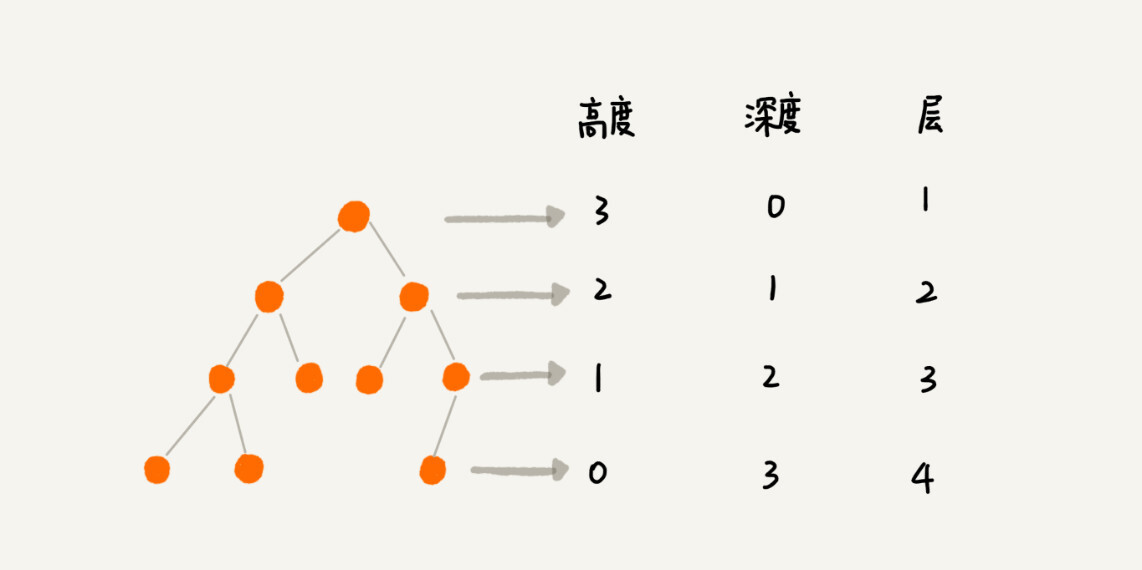
• 高度

  节点到叶子节点的最长路径(边数)

• 深度

  根节点到这个节点所经历的边的个数

• 层

  节点的深度+1

二叉树

---

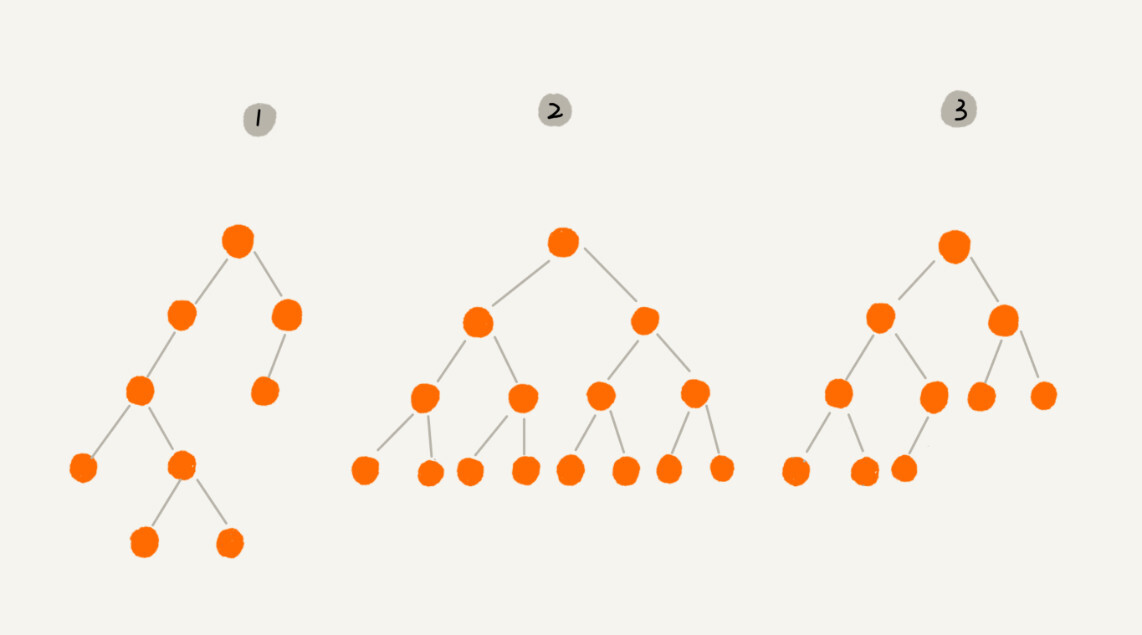
每个节点最多有两个节点,左右节点.

其中编号2是一个满二叉树,编号3则是一个完全二叉树(便于用数组表示).

二叉树的存储

---

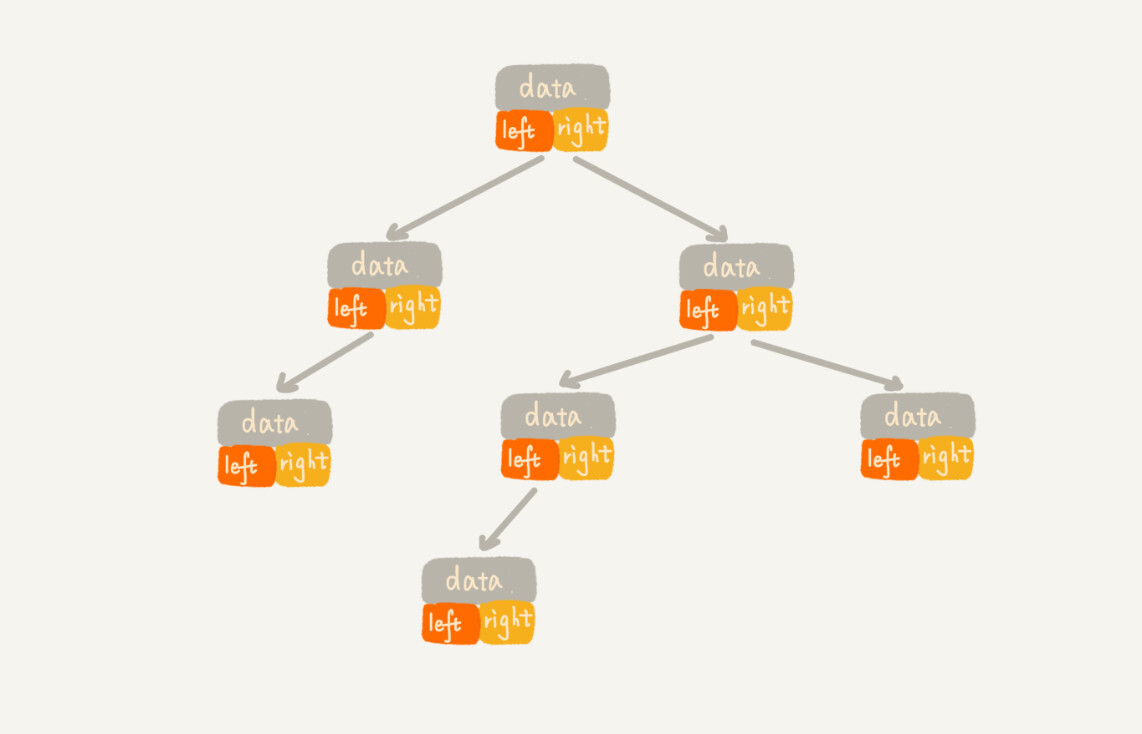
• 基于指针或引用的链式存储,大部分二叉树代码都是通过这种结构实现

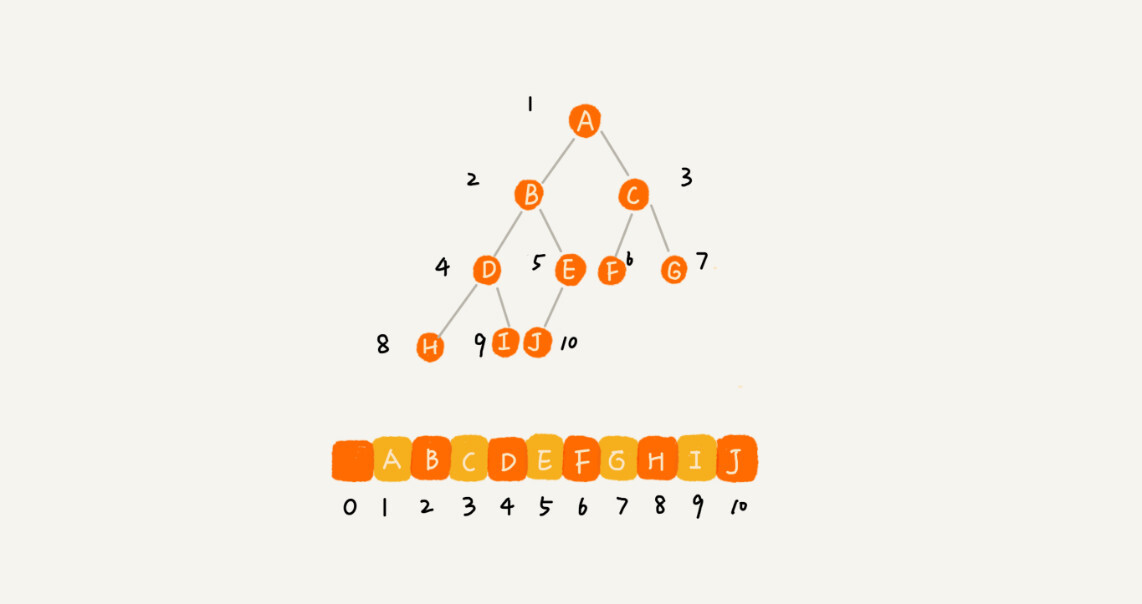
• 基于 数组 的顺序存储法,完全二叉树使用数组 顺序存储法 可以节省内存

完全二叉树 即 叶子节点分布在最后两层,并且最后一层的叶子节点靠左排列.

一般根节点放在数组下标为1的位置,便于计算.
如果该节点的下标为i,则它的左孩子下标为2*i,右孩子的下标为2*i+1;父节点的下标为i/2.

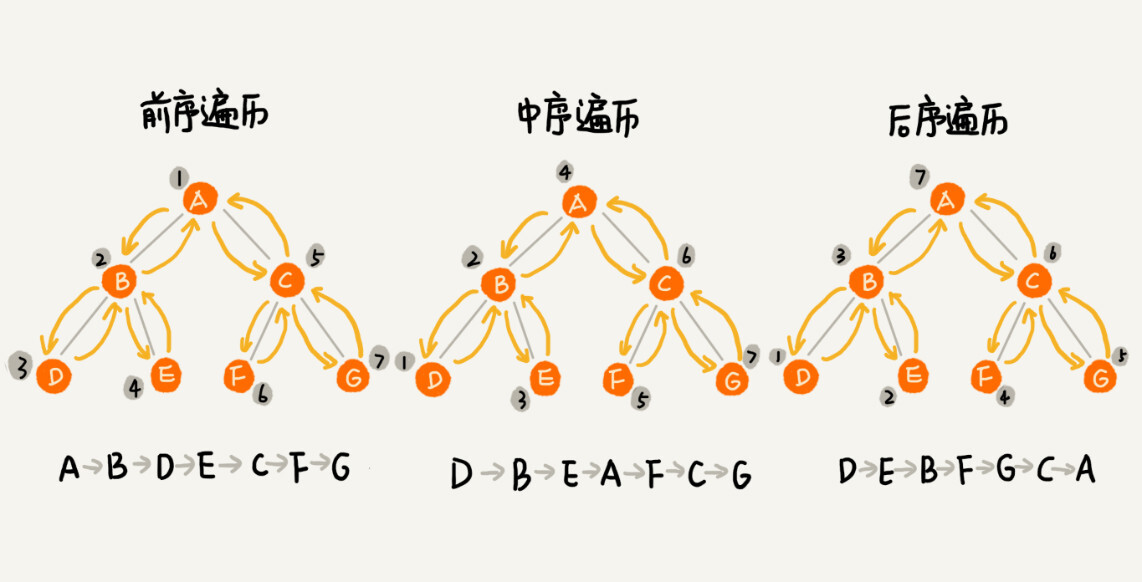
二叉树的遍历

---

• 前序遍历

  对于任意节点,先打印该节点,然后打印它的左右子树

• 中序遍历

  对于任意节点,先打印该节点的左子树,再打印该节点,最后打印该节点的右子树

• 后序遍历

  对应任意节点,先打印该节点的左右子树,最后打印该节点

• 层序遍历

  按每一层顺序打印,完全二叉树直接遍历数组即可

树的分类

---

二叉搜索树(Binary Search Tree)

二叉搜索树能够实现快速查找,快速插入和快速删除一个数据.O(logn)

二叉树的特殊结构:
    在树中的任意一个节点,其中左子树的每个节点的值都小于这个节点,右子树的每个节点都大于这个节点的值.

• 二叉树的查找操作

• 二叉树的插入操作

• 二叉树的删除操作

• 其他(快速查找最大节点和最小节点,排序)

  最大节点位于最右侧
  最小节点则位于最左侧
  排序操作,中序遍历,时间复杂度为 O(n),也称二叉排序树

• 既然散列表的插入,删除,查找操作的时间复杂度可以做到常量级的O(1),而二叉树在比较平衡的情况下插入删除查找操作的复杂度才是O(logn).为什么还要用二叉查找树?

  1.散列表是无序存储的,而二叉查找只需中序遍历即可.
  2.散列表扩容耗时很多,而且遇到散列冲突时,性能不稳定.
  3.hash冲突的存在,这个常量可能比树的logn大
  4.散列表的构造比树复杂:
      散列表需要考虑散列函数的设计,冲突解决方案,扩容,缩容等
      二叉查找树只需要考虑平衡性的问题,(AVL树,红黑树)